The effects of geoid changes in NGS’s new, modernized 2022 NSRS

My April column addressed the vertical movement at the NOAA CORS Network (NCN). The values at the sites indicate the potential movement of marks in the area of the CORS. The rates are based on GNSS data and have an estimate of error associated with them.

As I mentioned in my previous column, I’m not sure how the National Geodetic Survey (NGS) will address the vertical movement effects in the new, modernized National Spatial Reference System (NSRS). That said, NGS will be monitoring the CORS and looking for trends to help describe the vertical movement at the CORS. These trends are an indication of what may be happening in that area.

As stated in previous columns, orthometric heights in NAPGD2022 will be defined through ellipsoid heights and a geoid model, for example GEOID2022. In addition to the movement of individual marks due to crustal movement, there are geophysical reasons for changes in the geoid that affect the orthometric height of a mark. Therefore, changes in the geoid model will be very important to users estimating orthometric heights using GNSS.

As stated in the NOS NGS 64 report, NGS has set a goal of maintaining geoid accuracy at 1 centimeter (1 standard deviation) in both absolute and differential geoid undulations. The box titled “Figure 13 from NOS NGS 64 Report” depicts an estimate of the secular change in the geoid. As indicated in the plot, the changes are very small, ranging from -1.25 mm/year to 1.5 mm/year.

What I find interesting is the small negative change in the southeastern United States. There are other drivers for geoid changes. This column will address some of these changes and what they mean to users.

Secular geoid change

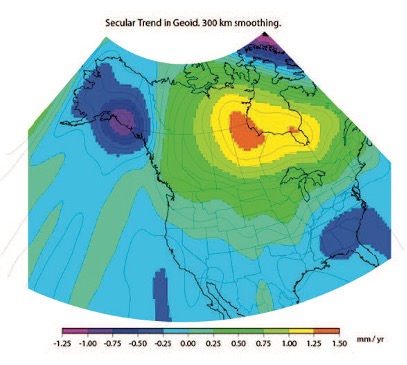
Figure 13 from NOS NGS 64 Report (Image: NGS)

As mentioned in many of my articles, the new, modernized NSRS has a time-dependent component. This includes the geoid model.  Table 5-1 from NOS NGS 64 report are examples of some of the physical processes being investigated by NGS to account for changes in the geoid.  (See the box titled “Some of the geophysical drivers of geoid change.”) As mentioned in the NOS NGS 64 report, the magnitudes in red have already been determined to be too small for NGS to model. The examples highlighted in yellow have magnitudes that are significant and NGS will attempt to account for these changes to the geoid. 

Table 5-1: Some of the geophysical drivers of geoid change

NGS classifies the changes in the geoid in three different groups: Shape Change, Size Change, and W₀ Change. The box titled “The Groups of Geoid Change” provides NGS’s definition and explanation of the terms.

The groups of geoid change

NGS’s report on their Geoid Monitoring Service (GeMS) program provides figures that depict an estimate of the secular geoid rate trend based on the NASA GSFC mascon model. See the boxes titled “Estimate of Geoid Rate Over CONUS” and “Estimate of Geoid Rate Over Alaska.” For more details on GeMS, download the report NOAA Technical Report NOS NGS 69: A Preliminary Investigation of the NGS’s Geoid Monitoring Service (GeMS), and read my December 2019 Survey Scene column. The secular geoid rate trend is an example of the geoid changing its shape, but not the W₀ value. What this means is that the local geoid undulations will change, but the overall size of the geoid will not.

Estimate of geoid rate over CONUS

Figure 32: Geoid rate over CONUS based on the GSFC mascon model [mm/yr] (Image: NOAA)

Figure 33: Geoid rate over Alaska from GSFC mascon model [mm/yr] (Image: NOAA)

In recent history, on May 18, 1980, geologists watched in awe as Mount St. Helens erupted in a gigantic explosion. After the eruption, the volcanic cone of Mount St. Helens had been completely blasted away; the peak, which was at an elevation of 9,677 feet (2,950meters) was changed to a horseshoe-shaped crater with an elevation of 8,363 feet (2,549 meters). Extreme crustal movements such as the Mount St. Helens eruption can change the shape of the geoid. As explained in my April 2022 newsletter, NGS understands this and is attempting to manage the changing coordinates by providing a time-dependent component to a mark’s ellipsoid height, but there is also a time-dependent component to the geoid that affects the mark’s orthometric height.

Ring of Fire

Image: National Ocean Service

The “Ring of Fire” map highlights earthquake activities around the world. As indicated in Table 5.1, earthquake or volcanic eruptions can change the shape of the geoid. Of course, they also can change the height of a mark due to crustal movement, which would typically be larger than the change in the geoid height. The amount of movement would be due to the size and magnitude of the event, but even small earthquakes could cause a change in the height of a mark located near the event. Earthquakes are occurring all over the world every day. 

Earthquakes with large magnitudes are highlighted by news media outlets, but ones with smaller magnitude typically are not highlighted. The four figures below provide examples of earthquakes that have occurred over 30 days. This information can be obtained from the United States Geological Survey (USGS).

Earthquakes during the past 30 Days
Date: May 20, 2022

Image: USGS

Earthquakes in the lower 48 during the past 30 days
Date: May 20, 2022

Image: USGS

Earthquakes in eastern United States in the past 30 days
Date: May 20, 2022

Image: USGS

I found the large number of earthquakes that occurred in Oklahoma in just 30 days to be very interesting.  This isn’t something that I thought occurred in the eastern region of the United States. 

Earthquakes in Oklahoma during the past 30 days
Date: May 20, 2022

Image: USGS

The image below depicts earthquakes that have occurred in Oklahoma in the past five years. They are fairly small in magnitude, but what is the cumulative effect on the geoid in the region, as well as changes to the orthometric heights of marks due to crustal moment in the region?  This is why it is important for the new, modernized NSRS to implement time-dependent coordinates. 

Earthquakes in Oklahoma in the last 5 years
Dates: 2017 to 2022

Image: USGS

To better understand the changes to the geoid, NGS performed a survey in Alaska to obtain geodetic data as part of its GeMS program.  On May 12, 2022, Kevin Ahlgren, a geodesist at NGS, described in a webinar the observations collected and some of the results. 

The presentation provided an overview of a field campaign performed in support of the GeMS program and a time-dependent geoid model. The campaign included static GNSS, relative gravity, and deflection of the vertical techniques on 50 stations in Alaska. The webinar was can be downloaded.

I encourage everyone to download the presentation.  The change in the geoid due to geophysical drivers is small, but if the new, modernized NSRS is going to include time-dependent coordinates, then changes in the geoid must be accounted for.  For demonstration purposes, NGS provides an example of the time-dependent geoid change in the xGEOID20 webtool.  The box below, “xGEOID20 interactive computation output,” is an example of using this tool. The two stations are located in Alaska. As indicated in the output from the tool, the change in the geoid is 8 mm in five years. Again, NGS’s goal is to maintain geoid accuracy at the centimeter level (1 standard deviation) in both absolute and differential geoid undulations.  These small changes can become significant over time. 

xGEOID20 interactive computation output

Note: DN is the time-dependent geoid change computed between user inputted epoch (t) and t. (Image: NGS)

The last geoid change group that I’ll highlight has to do with the change in the gravity potential (W₀) value that defines the model. The NOS NGS 64 Report states that the standing definition of the geoid, as adopted and used at NGS, is the following:  

The geoid is the equipotential surface of the Earth’s gravity field which best fits, in a least squares sense, global mean sea level. 

As stated in the NOS NGS 64 report, over a century of sea-level measurements imply that global mean sea level (GMSL) was rising at a rate of approximately 1.7 millimeters per year and was rising at a rate of 3.2 millimeters per year between 1993 and 2010 (IPCC, 2014). If NGS is going to define the geoid as the equipotential surface of the Earth’s gravity field that best fits, in a least squares sense, global mean sea level, then the geoid in the new, modernized NSRS must change when the GMSL exceeds a certain threshold. 

Again, NGS’ goal is to maintain geoid accuracy at the centimeter level (1 standard deviation) in both absolute and differential geoid undulations.  What this means is that as GMSL rises, the value of gravity potential which best fits to GMSL (called W₀) will also change.  In other words, the surface which was called “the geoid” and had W=W₀ in 2022 will no longer be the geoid. A new value of W₀ (W₀new) is chosen, and “the geoid” would now be the surface W=W₀new.   

So, what does this really mean to users? The NOS NGS 64 Report states on page 37:

“NGS and the Canadian Geodetic Survey have jointly adopted the value of 2.0 m^2/s^2 as the replacement threshold for a new geoid model (and new geopotential datum). This represents approximately 20 centimeters of GMSL (and thus geoid) rise. At the current rate of sea-level change of about +3 millimeters per year (IPCC, 2014), this means NGS expects to replace NAPGD2022 in approximately 60 to 70 years.” 

Therefore, this should not be a major concern of users for a long time. 

This column highlighted that orthometric heights in NAPGD2022 will be defined through ellipsoid heights and a geoid model, for instance GEOID2022; and therefore, changes in the geoid model will be very important to users estimating orthometric heights using GNSS.  It briefly described the geophysical reasons for changes in the geoid that affect the orthometric height of a mark. 

If NGS is going to meet the goal of maintaining geoid accuracy at 1 centimeter (1 standard deviation) in both absolute and differential geoid undulations, they will have to address changes in the geoid. The secular changes in the geoid, as indicated in Figure 13 in the NOS NGS 64 report, are very small, ranging from -1.25 mm/year to 1.5 mm/year. Once again, these are small changes to the geoid, but they will accumulate over time, and that is why NGS is including time-dependent coordinates in the new, modernized NSRS.