Antenna pattern uniformity effects on pseudorange tracking error

More satellites, more constellations, more multi-frequency receivers — they all drive greater achievable accuracy. But they also raise the requirements on GNSS antennas because of the stronger impact that possible imperfections might have in the overall error budget for multi-frequency combinations. This analysis of antenna-induced errors in pseudorange code measurements for different antenna feed types helps identify the advantages and disadvantages of such technologies for precise positioning.
By Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
The combination of signals from two frequencies and multiple constellations leads to dual-frequency multi-constellation (DFMC) capabilities, which currently appear to provide improved performance, due to the increased number of satellites available. This leads to better available satellite geometries, but also to the possibility to strongly mitigate ionosphere-related errors, thanks to dual-frequency combination of the ranging signals.
In such scenarios, the hardware-related errors (from satellite and even more from receiver side) will gain a much stronger weight in the overall error budget and should be tackled accordingly.
This article focuses mostly on the receiver antenna contribution, leaving the effects due to the satellite and to the receiver for later work. We will show that the choice of the antenna technology (mostly in terms of the number of feeding points) has a strong impact on the pattern uniformity and therefore on the differential group-delay characteristics over the aspect angle. Optimal performance is demonstrated when using more sophisticated solutions, providing a ground for cost/performance analysis to system engineers of specific applications.
GROUP DELAY PERFORMANCE
Antenna performance in GNSS application is mostly evaluated in terms of antenna gain pattern, noise figure and group delay for code measurement or phase center variation for carrier phase measurement. Gain and noise figure impact on the signal level available at the receiver, while the group delay is a measure of the delay introduced by the antenna hardware to the different spectral components of the signal. The differential group delay (DGD) is
with φ, f, Az, El being respectively the antenna phase, frequency, azimuth and elevation.
The DGD variation with respect to frequency and aspect angle (that is, elevation and azimuth) actually poses a problem in precision applications: as a matter of fact, if the group delay were constant for all frequencies and all angles of arrival of the signal, no additional error would be introduced in the position calculation, because the group delay term common to all satellites would be encapsulated at the receiver into a user clock offset.
However, group delay can change significantly with respect to aspect angle and frequency, contributing in a different manner for each satellite (due to different angles) and for different signals (due to the different spectral components of each signal), therefore finally producing errors in the pseudorange estimation.
The influence of the DGD on pseudorange measurement error has already been studied in the past and is also taken into consideration in the antenna Minimum Operational Performance Standards (MOPS) for avionic antennas. Empirical studies on the combined effect of antenna group delay and multipath effect on board commercial airplanes have been published recently. However, to our knowledge, the correlation between the antenna intrinsic characteristics (such as gain and phase patterns and smoothness) and group delay behavior has not yet been properly analyzed, leaving a gap in the full understanding of the antenna design impact on the final GNSS receiver performance.
GNSS antennas can be divided into families, according to their geometry (and the related radiation mechanisms): for instance, spiral, helix and microstrip (patch) antennas are quite common in GNSS applications.They differ in achievable bandwidth, size and ease of manufacturing.
Even antennas of the same family can provide different performance, mainly because of the number of feeding points, which are the points where the signal is fed into the antenna.
In order to analyze the relationship between the group delay performance and the antenna properties, we will take into consideration three GNSS antennas of the same family (microstrip patch), having all about half-effective-wavelength size (with the effective wavelength considering the dielectric properties of the substrate material on which the patch antenna is positioned), but with a different number of feeding points. The antennas will be denominated respectively single-feed, double-feed and four-feed antennas.
The single-feed antenna is a square patch, with truncated corners to achieve circular polarization. On the other hand, the double- and four-feed antennas are square patches, having feeds positioned along their x- and y-axis. The feeds are fed progressively: that is, with same amplitude and 0°–90° phases for the double feed and 0–90–180–270° phases for the four feed.
Single-feed antennas are representative of lower cost antennas used in mass-market applications, due to their extreme simplicity allowing for low-cost production. However, their performance exhibits strong cross polarization levels and non-uniform patterns over the azimuth. Dual- and four-feed antennas are more complicated to manufacture and need further hybrid circuits to properly distribute the signal between the different feeding points. However, an increase in the feeding points leads to more uniformity in the radiation pattern and lower-cross polarization and can therefore be expected to improve performance.
Dual-feed antennas are common in applications where a balance between precision and cost is needed, while four feeds are used in high-end applications, such as geodesy and reference stations.
The antennas under consideration here have been tuned to obtain optimal behavior at GPS L1/Galileo E1 band and have been simulated in an electromagnetic solver (Ansys HFSS), with an infinite ground plane assumption, to resemble the large metallic body frame of aircraft structures.
The gain patterns of the different antennas at GPS L1 / Galileo E1 central frequency ( f=1575 MHz) are shown in Figure 1. As discussed earlier, the pattern is not uniform over angle for the single-feed solution. On the other hand, the four-feed antenna shows improved pattern uniformity: the pattern has fewer azimuth and elevation variations, with the two-feed solution providing intermediate results.
- Figure 1a. 3D RHCP patterns at f=1575 MHz for single-feed antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
- Figure 1b. 3D RHCP patterns at f=1575 MHz for a dual-feed antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
- Figure 1c. 3D RHCP patterns at f=1575 MHz for a four-feed antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
Phase patterns for the three antennas are shown in Figure 2. Here again, the one-feed solution exhibits more angular variation than the multi-feed solutions. It is interesting to notice how strong phase variations occur in the same regions where the gain pattern also varies strongly.
- Figure 2a. 3D RHCP phase patterns at f=1575 MHz for a single-feed antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
- Figure 2b. 3D RHCP phase patterns at f=1575 MHz for a dual-feed antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
- Figure 2c. 3D RHCP phase patterns at f=1575 MHz for a our-feed antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
When considering the DGD, the frequency dependence of the phase pattern will have to be taken into account, according to Equation (1). To show the DGD variability with respect to the aspect angle, the standard deviation of the DGD over a 20-MHz bandwidth has been calculated (for each azimuth and elevation angle) and is shown in Figure 3, confirming the better behavior of the four-feed antenna.
- Figure 3a. 3D standard deviation (calculated over frequency) of the DGD for a) single-feed antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
- Figure 3b. 3D standard deviation (calculated over frequency) of the DGD for a dual-feed antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
- Figure 3c. 3D standard deviation (calculated over frequency) of the DGD for a four-feed antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
Figure 4 shows the group delay versus frequency and elevation (with different azimuth values being represented by curves with different colors) for the three typologies of antennas: such typology of figure contains all information about DGD variation versus frequency and angle and is first introduced in this article. For comparison, in the RTCA’s 2006 MOPS document for airborne antennas, for the sake of simplicity, either DGD variation versus angle at central frequency or DGD variation over frequency at zenith were considered, hence not fully covering the complete space {Frequency, Azimuth, Elevation}.
- Figure 4a. Differential group delay versus elevation angle and frequency (each color represents an azimuth value) for single-feed antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
- Figure 4b. Differential group delay versus elevation angle and frequency (each color represents an azimuth value) for a dual-feed antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
- Figure 4c. Differential group delay versus elevation angle and frequency (each color represents an azimuth value) for a four-feed antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
While the single-feed antenna in Figure 4 shows a big variation of the DGD when moving from zenith (that is, Elevation = 90°) to lower elevations, a substantial decrease in the DGD spread is recorded for the four-feed solution, with the dual-feed one having again intermediate results.
It is worthwhile noticing that the results obtained for the dual-feed solution are in agreement with the current MOPS for L1 antennas (RTCA DO-301), specifying a maximum value of 2.5 nansoseconds (ns) for the group delay spread at low elevations (normalized to boresight, El = 90°).
The results show how angular variation of the DGD can be related to non-uniformity along the aspect angle (Az or El) and frequency, hence suggesting to use multiple-feed solution for obtaining optimal performance.
A useful metric to quantify the uniformity of the group delay can be introduced as the Uniformity Indicator for Group Delay (UIGD):
with ![]() being the sum over frequency (Nf is the number of frequency steps considered) and DGDzenith,n being the value of the DGD at zenith for frequency n.
being the sum over frequency (Nf is the number of frequency steps considered) and DGDzenith,n being the value of the DGD at zenith for frequency n.
The UIGD expresses the maximum variation of the DGD over elevation and azimuth from a reference condition (the DGD at zenith) in the bandwidth of interest, extending de facto the MOPS requirements by considering the whole bandwidth behavior in the whole upper hemisphere.
The UIGD for the one-, two- and four-feed antennas is respectively 4.18, 1.03 and 0.05 ns, hence effectively mirroring the better pattern uniformity of the four-feed solution.
The UIGD is a comprehensive metric to describe the DGD uniformity, but needs accurate phase measurement over the entire bandwidth, which may not be always easily obtainable. As a matter of fact, phase can be challenging to measure: some indication of the areas most likely to deliver increased DGD can be found while considering gain patterns, qualitatively providing an easier metric to compare different antennas. In this case, the Uniformity Indicator for Gain (UIG)can be used:
The UIG expresses the maximum value over all elevation and azimuth angles of the standard deviation of the RHCP gain derivative over frequency (in the band of interest), therefore indicating the roughness of the antenna gain pattern in frequency and angle.
Such a metric does not relate totally with DGD behavior, but serves as an easier metric of pattern uniformity. The UIG for the one-, two- and four-feed antennas is respectively 68.5, 5.7 and 0.3%.
REAL-LIFE PERFORMANCE AND IMPACT ON ACCURACY
To evaluate the performance of actual antennas, three prototypes were measured in a Satimo Starlab anechoic chamber at the German Aerospace Center (DLR).
The antennas under test were:
- A badly polarized COTS active antenna, having a behavior similar to that of a single-feed antenna;
- An in-house developed passive antenna with two feeds;
- An in-house developed passive four-feed antenna.
All antennas were properly tuned to obtain optimal gain and minimum reflection losses (input reflection coefficient <–10 dB) at L1 /E1 central frequency.
The measured RHCP pattern for the various antennas is shown in FiGURE 5. The UIGD for these antennas is 0.9, 0.7 and 0.2 ns respectively, while the UIG is 46.6, 38.5 and 9.0%.
- Figure 5a. Measured 3D RHCP gain patterns at f=1575 MHz for a badly polarized COTS antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
- Figure 5b. Measured 3D RHCP gain patterns at f=1575 MHz for a DLR dual-feed antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
- Figure 5c. Measured 3D RHCP gain patterns at f=1575 MHz for a DLR four-feed antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
Differential group delay was calculated from the measured phase values and is shown in Figure 6.
- Figure 6a. Differential group delay versus elevation angle and frequency (each color represents an azimuth value) as from measurement for a badly polarized COTS antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
- Figure 6b. Differential group delay versus elevation angle and frequency (each color represents an azimuth value) as from measurement for a DLR dual-feed antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
- Figure 6c. Differential group delay versus elevation angle and frequency (each color represents an azimuth value) as from measurement for a DLR four-feed antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
The results are similar to those obtained from simulation and clearly show the improved flatness of the DGD for the four-feed case.
Moreover, if the measured phase data are fed into an ideal GNSS receiver, able to provide the tracking biases occurring in the pseudorange code measurement for all elevations and azimuths, antenna-effects-only (as weighted by the signal characteristics) will be visible (as in this case, neither multipath nor receiver or satellite imperfections are included in the ideal receiver). The results are shown in Figure 7.
- Figure 7a. Pseudorange bias versus elevation angle (each color represents an azimuth value) at L1 band for badly polarized COTS antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
- Figure 7b. Pseudorange bias versus elevation angle (each color represents an azimuth value) at L1 band for a DLR dual-feed antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
- Figure 7c. Pseudorange bias versus elevation angle (each color represents an azimuth value) at L1 band for a DLR four-feed antenna. Source: Stefano Caizzone, Mihaela-Simona Circiu, Wahid Elmarissi, Christoph Enneking, Michael Felux and Kazeem A. Yinusa, German Aerospace Center (DLR)
A substantial decrease in the antenna-induced error is evident as expected when the four-feed antenna is used.
The differences in performance among different antenna technologies shown here provide valuable insight in the choice of the antenna technology for a specific application, thanks to the better understanding of the impact of the antenna characteristics on the error at pseudorange level. Moreover, they can support the evaluation and definition of antenna requirements and connect them to the expected GNSS pseudorange error, such as during the process of MOPS definition as currently occurring for DFMC systems.
CONCLUSIONS
After investigating the effects of pattern uniformity on antenna-induced errors, group delay behavior over aspect angle and frequency has been shown comprehensively for different antenna feeding technologies for the first time. Minimal error in pseudorange measurements is obtained when the antenna has a smooth pattern, with no abrupt variations or nulls/sidelobes both in aspect angle and frequency. Different antenna feeding technologies currently in use for circularly polarized radiation have been evaluated, and the best performing one has been identified in the multiple-feed solution.
Both a comprehensive and an easier-to-measure metric for group delay uniformity have been identified, providing useful insight for fast comparison of the performance of multiple antennas in terms of GNSS accuracy.
STEFANO CAIZZONE received a Ph.D. in geoinformation from the University of Rome, Tor Vergata. He is is responsible for the development of innovative miniaturized antennas in the antenna group of the Institute of Communications and Navigation of the German Aerospace Center (DLR).
MIHAELA-SIMONA CIRCIU received a master’s degree in computer engineering from Technical University Gheorghe Asachi, Romania, and a master’s in navigation and related applications from Politecnico di Torino, Italy. She works on the development of the multi-frequency multi-constellation Ground Based Augmentation System for DLR.
WAHID ELMARISSI received a Dipl. Ing. in electrical engineering from the University of Applied Sciences, Kiel, Germany. He is responsible for measurement and manufacturing of antennas and antenna electronics at DLR.
CHRISTOPH ENNEKING received a MSc. degree in electrical engineering from the Munich University of Technology. He conducts research in GNSS signal design, estimation theory and GNSS intra- and inter-system interference at DLR.
MICHAEL FELUX is a research associate specializing in GBAS integrity issues for CAT -II/III operations and program manager for the research on GBAS navigation at DLR. He graduated in technical mathematics at Technische Universität München.
KAZEEM A. YINUSA received MSc. and Dr.-Ing. degrees in electrical engineering from the Technische Universität München. He is a researcher at DLR.













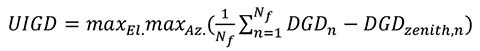
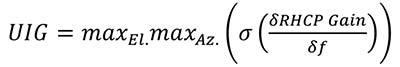























Follow Us